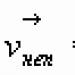Равновесие тела при наличии трения скольжения. Равновесие твердого тела при наличии трения качения Понятие о ферме. Аналитический расчет плоских ферм

то задача становится статически неопределимой (для ее решения необходимо привлечь какие-либо соображения, выходящие за рамки наших представлений о твердых телах).

Пример 1.16 . На шероховатой наклонной плоскости, составляющей угол = 30° с горизонтальной плоскостью, находится тело весом Р = 20 Н (рис. 1.53,а). Тело удерживается на плоскости тросом АВ, весом которого можно пренебречь. Определить силу трения Т между телом и плоскостью и минимальное натяжение троса при двух значениях коэффициента трения f 1 =0,8 и f 2 =0,2 .

На тело действуют четыре силы: активная сила – сила тяжести , сила трения , нормальная составляющая реакции плоскости и реакция троса (рис. 1.53,6). Введем систему координат и составим условия равновесия тела

∑F ix = Psin – T - S = 0; ∑F iy =N – Pcos = 0;

T ≤f ·N.

Отсюда найдем

S = Psin – T; N = Pcos ; T ≤ f · Pcos ,

Или, учитывая условия задачи,

S = 10-T ; T ≤ 17,3·f .

Для первого случая f 1 =0,8, поэтому будем иметь T≤ 13,8Н. При отсутствии троса (S = 0) получим T =10Н. Так как при этом условие Г<13,8Н не нарушается, то это означает, что при f 1 =0,8 тело будет находиться в равновесии за счет одной силы трения Т =10 Н.

Пусть теперь f 2 = 0,2. Тогда должно выполняться условие T≤ 17,3 · f 2 =3,46Н. При отсутствии троса (S = 0) это неравенство находится в противоречии с первым уравнением 10-T = 0. Это означает, что при отсутствии троса тело начало бы скользить вниз. Поэтому при f 2 = 0,2 сила трения достигает своего максимального значения, равного Т = 3,46 Н, а натяжение троса будет S =10-7 = 6,54 Н.

Итак, при f 1 =0,8: T =10Н, S =0;

при f 2 =0,2: T = 3,46Н, S =6,54Н.

Пример 1.17. На наклонной плоскости находится цилиндр (рис. 1.54). Найти, при каких углах наклона плоскости к горизонту цилиндр будет находиться в равновесии, если R – радиус цилиндра, f –коэффициент трения скольжения, δ – коэффициент трения качения, Р – вес цилиндра .

На цилиндр действуют: активная сила тяжести , нормальная сила реакции в точке контакта , касательная составляющая реакции в точке контакта (сила трения), пара сил с моментом трения качения M T (рис. 1.54).

Сначала нарушится неравенство (1.79), если же f < , то нарушится неравенство (1.78) и цилиндр начнет скользить.

Рассмотрим цилиндр (каток), покоящийся на горизонтальной плоскости, когда на него действует горизонтальная активная сила S;кроме нее, действует сила тяжести Р, а также нормальная реакция N и сила трения Т (рис. 6.10, а). Как показывает опыт, при достаточно малой величине силы S цилиндр остается в покое. Но этот факт нельзя объяснить, если удовлетвориться введением сил, изображенных на рис. 6.10, а. Согласно этой схеме равно­весие невозможно, так как главный момент всех сил, действую­щих на цилиндр Mcz : = - Sr , отличен от нуля и одно из условий равновесия не выполняется.

Причина выявившегося несоответствия состоит в том, что в наших рассуждениях мы продолжаем пользоваться представ­лением об абсолютно твердом теле и предполагаем касание цилиндрас поверхностью происходящим по образующей. Для устранения отмеченного не­соответствия теории с опы­том необходимо отказаться от гипотезы абсолютно твердого тела и учесть, что в действительности ци­линдр и плоскость вблизи точки С деформируются и существует некоторая пло­щадь соприкосновения ко­нечной ширины. Вслед­ствие этого в ее правой части цилинлр прижимает­ся сильнее, чем в левой, и полная реакция R при­ложена правее точки С (см. точку С 1 на рис. 6.10, б). Полученная теперь схе­ма действующих сил ста­тически удовлетворитель­на, так как момент пары (S, Т) может уравновеситься моментом пары (N, Р). Считая де­формацию малой, заменим эту систему сил системой, изображен­ной на рис. 6.7, в. В отличие от первой схемы (рис. 6.10, а), к цилиндру приложена пара сил с моментом Мт=Nh (6.11)

Этот момент называется моментом трения качения. Составим уравнения равновесия цилиндра: S-T=0, N-P=0, -Sr+Mt=0 (6-12)

Первые два, уравнения дают T=S, N = P , а из третьего урав­нения можно найти М Т. Затем из (6.11) определяем расстояние между точками С и С1: h = Sr / P (6.13)

Как видно, с увеличением модуля активной силы S растет рас­стояние h. Но это расстояние связано с площадью поверхности контакта и, следовательно, не может неограниченно увеличи­ваться. Это значит, что наступит такое состояние, когда увели­чение силы S приведет к нарушению равновесия. Обозначим максимально возможную величину h буквой δ (см. рис. 6.10, б). Экспериментально установлено, что величина δ пропорциональна радиусу цилиндра и различна для разных материалов.

Следовательно, если имеет место равновесие, то выполняется условие h≤δ (6.14)

Величина δ называется коэффициентом трения качения; она имеет размерность длины. Условие (6.14) можно также запи­сать в виде Mт≤δN(6.15)

или, учитывая (6.12), S ≤δN/r (6.15)

Очевидно, что максимальный мо­мент трения качения Mтmax = 8 N про­порционален силе нормального давления. В справочных таблицах приводится отношение коэффициента трения качения к радиусу цилиндра (К = 8/г) для различных материалов

38. Чистый сдвиг

Ч
истый сдвиг - напряженное состояние, при котором по взаимно перпендикулярным площадкам (граням) элемента возникают только касательные напряжения. Касательные напряжения τ=Q/F, где Q - сила, действующая вдоль грани, F - площадь грани. Площадки, по которым действуют только касательные напряжения, называются площадками чистого сдвига. Касательные напряжения на них - наибольшие. Чистый сдвиг можно представить как одновременное сжатие и растяжение, происходящее по двум взаимно перпендикулярным направлениям. Т.е. это частный случай плоского напряженного состояния, при котором главные напряжения: σ 1 =-σ 3 σ 2 =0 Главные площадки составляют с площадками чистого сдвига угол 45 о.

При деформации элемента, ограниченного площадками чистого сдвига, квадрат превращается в ромб.  - абсолютный сдвиг,   δ/а - относительный сдвиг или угол сдвига .

Закон Гука при сдвиге :γ=τ/G или τ=Gγ. G - модуль сдвига или модуль упругости второго рода [МПа] - постоянная материала, характеризующая способность сопротивляться деформациям при сдвиге.G=E/2(1+µ) (Е - модуль упругости, - коэффициент Пуассона).

Потенциальная энергия при сдвиге: U=δQ/V=Q 2 a/2GF.

Удельная потенциальная энергия деформации при сдвиге: u=U/V=Q 2 a/2GFaF ,где V=аF - объем элемента. Учитывая закон Гука, u=τ 2 /2G.

Вся потенциальная энергия при чистом сдвиге расходуется только на изменение формы, изменение объема при деформации сдвига равно нулю.

напряженность

τ=P/ℓδ τ =M вн /2πR 2 δ σ α = τ ABsinα+ τ BCcosα σ τ α = τ ABcosα- τ BCsinα

AB=AC cos α, BC=AC sin α.

Отсюда следует, что: σ α = τ sin2α τ α = τ cos2α

15. Центр тяжести твердого тела – точка, неизменно связанная с этим телом, через которую проходит линия действия равнодействующей сил тяжести частиц тела при любом положении тела в пространстве. При этом поле тяжести считается однородным, т.е. силы тяжести частиц тела параллельны друг другу и сохраняют постоянную величину при любых поворотах тела. Координаты центра тяжести:

;
;
, где Р=р k , x k ,y k ,z k – координаты точек приложения сил тяжести р k . Центр тяжести – геометрическая точка и может лежать и вне пределов тела (например, кольцо). Центр тяжести плоской фигуры:

, F k – элементарная площадка, F – площадь фигуры. Если площадь нельзя разбить на несколько конечных частей, то
. Если однородное тело имеет ось симметрии, то центр тяжести тела находится на этой оси. Центр тяжести: дуги окружности с центральным углом 2:
; кругового сектора:
; треугольник: в точке пересеч. медиан (1/3 медианы от основания).

Статический момент площади плоской фигуры – сумма произведений элементарных площадей, входящих в состав площади фигуры, на алгебраические значения расстояний до некоторой оси. S x =y i F i = Fy c ; S y =x i F i = Fx c .

Вспомогательные теоремы для определения положения центра тяжести:

Т.1. Если однородное тело имеет ось симметрии, то центр тяжести тела находится на этой оси.

Т.2. Если однородное тело имеет плоскость симметрии, то его центр тяжести находится в этой плоскости.

Т.3. Объем тела вращения, полученного вращением плоской фигуры вокруг оси, лежащей в плоскости фигуры, но не пересекающей ее, равен произведению площади фигуры на длину окружности, описанной ее центром тяжести, V=2x c F.

Т
.4. Площадь поверхности вращения, полученной вращением плоской кривой вокруг оси, лежащей в плоскости этой кривой, но не пересекающей ее, равна произведению длины этой кривой на длину окружности, описанной ее центром тяжести,F=2x c L.

Определяя положение центра тяжести плоской фигуры с вырезанной из нее частью, можно считать площадь этой части отрицательной и тогда:
и т.д. - способ отрицательных площадей (объемов).

24.Теорема о сложении скоростей :
,; рчастныепоэтому скорость его конца
и т.д.,: ,

; – относительная скорость.

; переносная скорость:
, поэтому абсолютная скорость точки = геометрической сумме ее переносной (v e) и относительной (v r) скоростей
, модуль:.

Выбираем систему координатных осей Oxyz (рис. 48) и вычисляем проекции главного вектора как алгебраические суммы проекций всех заданных сил на выбранные оси:

По найденным проекциям, откладывая соответствующие отрезки вдоль координатных осей (с учетом знака проекции), строим прямоугольный параллелепипед. Направленная диагональ, проведенная из начала координат в противоположную вершину параллелепипеда, определяет главный вектор R (см. также рис. 26).

Модуль и направляющие косинусы главного вектора определяются следующими вытекающими из построения формулами:

Совершенно аналогично определяются проекции, модуль и направляющие косинусы главного момента:

К формулам для вычисления проекций главного момента необходимо привести следующие пояснения.

Главный момент, по определению, есть векторная сумма моментов всех сил центра О. Следовательно, его проекции на координатные оси равны алгебраическим суммам проекций на эти оси векторов-моментов сил относительно центра О, то есть величин

Но эти величины, по определению момента силы относительно оси, являются моментами сил относительно соответствующих координатных осей:

Отсюда непосредственно следуют написанные выше выражения для величин .

Косинус угла между главным вектором и главным моментом определяется так:

Формула получается следующим образом. По определению скалярного произведения векторов R и имеем:

С другой стороны, эта же величина может быть вычислена через проекции векторов-сомножителей:

Приравнивая правые части и разрешая полученное уравнение относительно coscp, приходим к написанной формуле.

Условия равновесия произвольной плоской системы сил. Случай параллельных сил.

Для равновесия любой плоской системы сил необходимо и достаточно, чтобы одновременно выполнялись условия: R = 0, M 0 = 0.

Здесь О - любая точка плоскости.

Найдем вытекающие из равенств аналитические условия равновесия.

Величины R и М о определяются равенствами:

Равенства выражают, следующие аналитические условия рав­новесия: для равновесия произвольной плоской системы сил, необходимо и достаточно, чтобы суммы проекций всех сил на каж­дую из двух координатных осей и сумма их моментов относительно любого центра, лежащего в плоскости действия сил, были равны нулю.

Теорема о трех моментах. Для равновесия плоской системы сил, действующих на твердое тело, необходимо и достаточно, чтобы суммы моментов этих сил системы относительно трех любых точек, расположенных в плоскости действия сил и не лежащих на одной прямой, были равны нулю.

Равновесие плоской системы параллельных сил.

В случае, когда все действующие на тело силы параллельны друг другу, мы можем направить ось Ох перпендикулярно к силам, а ось Оу параллельно им (рис. 29). Тогда проекция каждой из сил на Ox будет равна нулю и первое из 3-х равенств обратится в тождество вида 0 = 0. В результате для параллельных сил останется два условия равновесия:

Где ось Оу параллельна силам.

11. Равновесие тела при наличии трения скольжения

Если два тела I и II (рис. 6.1) взаимодействуют друг с другом, соприкасаясь в точке А, то всегда реакцию R A , действующую, например, со стороны тела II и приложенную к телу I, можно раз­ложить на две составляющие: N A , направленную по общей нормали к поверхности соприкасающихся тел в точке А, и Т А, лежащую в касательной плоскости. Составляющая N A называется нормальной реакцией, сила Т А называется силой трения скольжения - она препятствует скольжению тела I по телу II. В соответствии с аксио­мой 4 (третьим законом Ньютона) на тело II со стороны тела I дей­ствует равная по модулю и противоположно направленная сила реакции. Ее составляющая, перпендикулярная касательной пло­скости, называется силой нормального давления. Сила трения Т А = 0, если соприкасающиеся поверхности идеально гладкие. В реальных условиях поверхности шероховаты и во многих случаях пренебречь силой трения нельзя. Максимальная сила трения приближенно пропорциональна нормальному давлению, т. е. T max =fN. (6.3)– закон Амонтона-Кулона. Коэффициент f называется коэффициентом трения скольжения. Его значение не зависит от площади соприкасающихся поверхностей, но зависит от материала и степени шероховатости соприкасающихся поверх­ностей. Силу трения можно вычислить по ф-ле T=fN только если имеет место критический случай. В других случаях силу трения следует определять из ур-ий равнов. На рисунке показана реакция R (здесь активные силы стремятся сдвинуть тело вправо). Угол j между предельной реакцией R и нормалью к поверхности называется углом трения. tgj=T max /N=f.

Геометрическое место всех возможных направлений предельной реакции R образует коническую поверхность - конус трения (рис. 6.6, б). Если коэффициент тре­ния f во всех направлениях одинаков, то конус трения будет круговым. В тех случаях, когда коэффициент трения f зависит от направления возможного движения тела, конус трения не будет круговым. Если равнодействующая активных сил. нахо­дится внутри конуса трения, то увеличением ее модуля нельзя нарушить равновесие тела; для того чтобы тело начало движение, необходимо (и достаточно), чтобы равнодействующая активных сил F находилась вне конуса трения. Рассмотрим трение гибких тел (рис.6.8). Формула Эйлера помогает найти наименьшую силу P, способную уравновесить силу Q. P=Qe -fj* . Можно так же найти такую силу P, способную преодолеть сопротивление трения вместе с силой Q. В этом случае в формуле Эйлера поменяется только знак f: P=Qe fj* .

Равновесие при наличии трения скольжения

При скольжении тела по шероховатой поверхности возникает сила реакции, которая имеет две составляющие – нормальную и силу трения скольжения (рисунок 2.1). Сила трения скольжения, приложенная к одному из трущихся тел, направлена противоположно его скорости относительно второго тела.

Рисунок 2.1

В результате экспериментальных исследований были установлены законы Амонтона-Кулона :

1) сила трения скольжения находится в общей касательной плоскости соприкасающихся поверхностей тел и направлена в сторону, противоположную направлению возможного скольжения тела под действием активных сил. Величина силы трения зависит от активных сил и заключена между нулем и своим максимальным значением, которое достигается в момент выхода тела из положения равновесия (0 ≤ F тр ≤ F тр max );

2) максимальное значение силы трения скольжения не зависит от площади контакта, а определяется величиной нормальной реакции, материалом и состоянием контактирующих поверхностей;

F тр max = fN ,

где f – коэффициент трения скольжения , который является безразмерной величиной и зависит от материала и физического состояния трущихся поверхностей, а также от скорости движения тела и удельного давления.

Экспериментально установлено, что f < f сц .

Рассмотрим твердое тело на шероховатой поверхности (рисунок 2.2), находящееся под действием активных сил в предельном состоянии равновесия, т.е. когда сила трения достигает своего наибольшего значения при данном значении нормальной реакции.

В этом случае полная реакция шероховатой поверхности отклонена от нормали к общей касательной плоскости трущихся поверхностей на наибольший угол (R max ). Этот наибольший угол между полной реакцией, построенной на наибольшей силе трения при данной нормальной реакции и направлением нормальной реакции, называется углом трения φ :

tgφ = F тр max /N = fN/N = f .

Рисунок 2.2

Рисунок 2.3

Конус трения – поверхность, образованная линией действия максимальной реакции опорной поверхности при движении тела в различных направлениях (рисунок 2.2).

При равновесии тела на шероховатой поверхности под действием силы P (рисунок 2.3) можно составить два уравнения равновесия:

ΣF kx = 0 ; Psinα - F тр = 0 ;

ΣF ky = 0 ; - Pcosα + N = 0 .

Следовательно,

Для равновесия тела на шероховатой поверхности необходимо и достаточно, чтобы линия действия равнодействующей активных сил, действующих на тело, проходила внутри конуса трения или по его образующей через его вершину.

Никакая сила, лежащая внутри конуса трения, не может вывести тело из состояния равновесия.

Трением качения называется сопротивление, возникающее при качении одного тела по поверхности другого. Вследствие деформации тел их касание происходит вдоль площадкиAB (рисунок 2.4, а), появляется распределенная система сил реакции (рисунок 2.4, б), которая может быть заменена силой и парой (рисунок 2.4, в).

Сила раскладывается на две составляющие – нормальную и силу трения скольжения. Пара сил называется моментом сопротивления качению M c .

Рисунок 2.4

При равновесии тела момент сопротивления качению определяется из условий равновесия системы сил. При этом установлено, что момент сопротивления принимает значения от нуля до максимального значения. Максимальное значение момента сопротивления, соответствующее началу качения, определяется равенством

M c max = Nδ ,

где δ – коэффициент трения качения , имеет размерность длины [м], зависит от материала контактирующих тел и геометрии зоны контакта.

Различают:

чистое качение – точка A (рисунок 2.4) не скользит по неподвижной плоскости;

качение со скольжением – наряду с вращением катка присутствует и проскальзывание в месте контакта, т.е. точка A движется по плоскости;

чистое скольжение – каток движется по плоскости, не имея вращения (см. п.2.1).

Для того, чтобы каток не скользил, необходимо условие F тр < F тр max ; чтобы каток не катился – M c < M c max = δN .

Также существует трение верчения – когда активные силы стремятся вращать тело вокруг нормали к общей касательной поверхности соприкосновения.

Изучение равновесия тел с учетом трения сводится обычно к рассмотрению предельного положения равновесия, когда сила трения достигает своего наибольшего значения. При аналитическом решении задач реакцию шероховатой связи в этом случае изображают двумя составляющими N и, где. Затем составляют обычные условия равновесия статики, подставляют в них вместо величину и, решая полученные уравнения, определяют искомые величины.

Пример 1. Рассмотрим тело, имеющее вертикальную плоскость симметрии (рис.28). Сечение тела этой плоскости имеет форму прямоугольника. Ширина тела равна 2a .

К телу в точке С , лежащей на оси симметрии, приложена вертикальная сила и в точке А , лежащей на расстоянии от основания, горизонтальная сила. Реакция плоскости основания (реакция связи) приводится к нормальной реакции и силе трения. Линия действия силы неизвестна. Расстояние от точки С до линии действия силы обозначим x ().

Составим три уравнения равновесия:

Согласно закону Кулона, т.е. . (1)

Проанализируем полученные результаты:

Будем увеличивать силу.

Если, то равновесие будет иметь место до тех пор, пока сила трения не достигнет своей предельной величины, условие (1) превратится в равенство. Дальнейшее увеличение силы приведет к скольжению тела по поверхности.

Если, то равновесие будет иметь место до тех пор, пока сила трения не достигнет величины, условие (2) превратится в равенство. Величина x будет равна h . Дальнейшее увеличение силы приведет к тому, что тело станет опрокидываться вокруг точки B (скольжения не будет).

Пример 2. На какое максимальное расстояние а может подняться человек по лестнице, приставленной к стене (рис.29)? Если вес человека - Р , коэффициент трения скольжения между лестницей и стеной - , между лестницей и полом - .

Рассматриваем равновесие лестницы с человеком. Показываем силу, нормальные реакции и и добавляем силы трения: и. Полагаем, что человек находится на расстоянии, при большем значении которого начнётся движение лестницы. Составляем уравнения равновесия.

Подставив значения сил трения и решив систему уравнений, получи

Теперь можно определить и угол под которым надо поставить лестницу, чтоб добраться до стены. Полагая, получим, после преобразований

Заметим, что если равнодействующая всех активных сил (всех кроме реакций) направлена под углом (рис.30), то нормальная реакция, а сила трения. Для того, чтобы началось скольжение должно выполнятся условие. или. И так как , то. Значит угол должен быть больше угла. Следовательно, если сила действует внутри угла или конуса трения (), то как бы не была велика эта сила, скольжение тела не произойдёт. Такое условие называется условием заклинивания, самоторможения.

Мы рассмотрели скольжение твёрдых тел по поверхности. Но нередко встречается скольжение гибких тел по неплоской поверхности. Например, нежелательное проскальзывание в ременной передаче ремня по шкиву, или троса, каната, намотанного на неподвижный цилиндр.

Пример 3. Пусть имеется нить, перекинутая через неподвижную цилиндрическую поверхность (рис.31). За счёт сил трения натяжение левого и правого концов этой нити будут различными.

Рис. 31

Предположим, что нормальная реакция и сила трения распределяются равномерно по дуге контакта нити на цилиндре. Рассмотрим равновесие участка нити длиной. (рис.32). На левом конце этого участка натяжение, на правом. Составляем уравнения равновесия, проектируя силы на оси:

Так как угол - малая величина, то полагаем С учётом этого из уравнений находим и, так как, имеем или Интегрируя, получим. Или

Этот результат называется формулой Эйлера.

Например, если нить перекинута через неподвижный шкив и, а коэффициент трения, то отношение натяжений. А, обернув цилиндр один раз (), то есть можно удержать груз на другом конце нити силой почти в три раза меньшей веса тела.

Изучение равновесия тел с учетом трения сводится обычно к рассмотрению предельного положения равновесия, когда сила трения достигает своего наиболь­шего значения . При аналитическом решении задач реакцию шероховатой связи в этом случае изображают двумя составляющимиN и , где. Затем составляют обычные условия равновесия статики, подставляют в них вместо величинуи, решая полу­ченные уравнения, определяют искомые величины.

Пример 1.

Рассмотрим тело, имеющее вертикальную плоскость симметрии (рис.28). Сечение тела этой плоскости имеет форму прямоугольника. Ширина тела равна 2a .

К телу в точке С , лежащей на оси симметрии, приложена вертикальная сила и в точкеА , лежащей на расстоянии от основания, горизонтальная сила. Реакция плоскости основания (реакция связи) приводится к нормальной реакциии силе трения. Линия действия силынеизвестна. Расстояние от точкиС до линии действия силы обозначимx ().

Рис.28

Составим три уравнения равновесия:

Согласно закону Кулона , т.е.. (1)

Так как , то(2)

Проанализируем полученные результаты:

Будем увеличивать силу .

Если , то равновесие будет иметь место до тех пор, пока сила трения не достигнет своей предельной величины, условие (1) превратится в равенство. Дальнейшее увеличение силы приведет к скольжению тела по поверхности.

Если , то равновесие будет иметь место до тех пор, пока сила трения не достигнет величины, условие (2) превратится в равенство. Величинаx будет равна h . Дальнейшее увеличение силы приведет к тому, что тело станет опрокидываться вокруг точки B (скольжения не будет).

Пример 2.

На какое максимальное рас­стояние а может подняться человек по лестнице, приставленной к стене (рис.29)? Если вес чело­века – Р , коэффициент трения скольжения между лестницей и стеной – , между лестни­цей и полом –.

Рис.29

Рассматриваем равновесие лестницы с че­ловеком. Показываем силу , нормальные реак­цииии добавляем силы трения:и. Полагаем, что чело­век находится на расстоянии, при большем значении которого начнётся движение лестницы. Состав­ляем уравнения равновесия.

Подставив значения сил трения и решив систему уравнений, получим

Теперь можно определить и угол под которым надо поставить лестницу, чтоб добраться до стены. Полагая , получим, после преобразований,и

Рис.30

Заметим, что если равнодействующая всех активных сил (всех кроме реакций) направлена под углом(рис.30), то нормальная реакция, а сила трения. Для того, чтобы началось скольжение должно выполнятся условие. или. И так как, то . Значит угол должен быть больше угла. Следовательно, если силадействует внутри угла или конуса трения (), то как бы не была ве­лика эта сила, скольжение тела не произойдёт. Такое условие называется усло­вием заклинивания, самоторможения.

Мы рассмотрели скольжение твёрдых тел по поверхности. Но нередко встречается скольжение гибких тел по неплоской по­верхности. Например, нежелательное проскальзывание в ременной передаче ремня по шкиву, или троса, каната, на­мотанного на неподвижный цилиндр.

Пример 3.

Пусть имеется нить, перекинутая че­рез неподвижную цилиндрическую поверх­ность (рис.31). За счёт сил трения натяже­ние левого и правого концов этой нити бу­дут различными.

Рис.31 Рис.32

Предположим, что нормальная реак­ция и сила трения распределяются равно­мерно по дуге контакта нити на цилиндре. Рассмотрим равновесие участка нити дли­ной . (рис.32). На левом конце этого участка натяжение, на пра­вом. Составляем уравнения равновесия, проектируя силы на оси:

Так как угол - малая величина, то полагаемС учётом этого из уравнений находими, так как, имеемилиИнтегрируя, получим. Или

Этот результат называется формулой Эйлера.

Например, если нить перекинута через неподвижный шкив и , а ко­эффициент трения, то отношение натяжений. А, обернув цилиндр один раз (),то есть можно удержать груз на другом конце нити силой почти в три раза меньшей веса тела.

Буддизм - культура индии Буддисты в индии

«Стожки» из фарша, рецепт с грибами — нежные, сочные, словами не передать!